| 编者按:一张好图胜过千言万语。如果可以使用简单易懂的可视化图表表达城市研究中各种复杂的对象和数据,那将会极大地帮助人们更好的认识城市。但如何才能做出一张好图?如何表示四维以上的数据?本期《城市科学文摘》介绍了一般数据的可视化,内容不仅包括柱状图、散点图等基本图表,也包括树图、桑基图等高级图表。本期文摘的大部分插图及有关“简洁”可视化的观点来自于Stephen Thomas 的著作Data Visualization with JavaScript和d3js.org的示例展示。 |
“When you consider the ultimate purpose of data visualization—helping users understand data—simplicity is one of the most important features of an effective visualization.”( “数据可视化的最终目标——是帮助用户理解数据,从这个意义上说,‘简洁’是有效数据可视化的最重要的特征之一。” )
基本图表 [注释1-2]
Bar Chart柱状图适用场合是二维数据集(每个数据点包括两个值x和y),但只有一个维度需要比较。柱状图利用柱子的高度,反映资料的差异。肉眼对高度差异很敏感,辨识效果非常好。柱状图的局限在于只适用中小规模的数据集。通常来说,柱状图的X轴是时间维,用户习惯性认为存在时间趋势(图1a)。如果遇到X轴不是时间维的情况,建议用颜色区分每根柱子,改变用户对时间趋势的关注。图1b是英国足球联赛某个年度各队的赢球场数,X轴代表不同球队,Y轴代表赢球数。
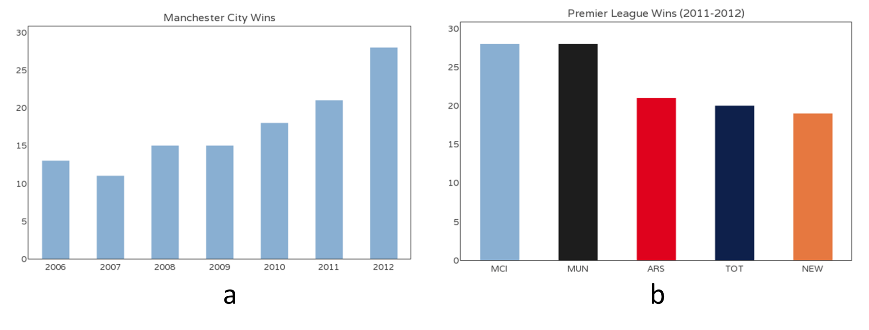
图1 柱状图 [注释1]
Line Chart折线图适合二维的大数据集,尤其是那些趋势比单个数据点更重要的场合。还适合多个二维数据集的比较。图2是两个二维数据集(大气CO2,地表平均气温)的折线图。
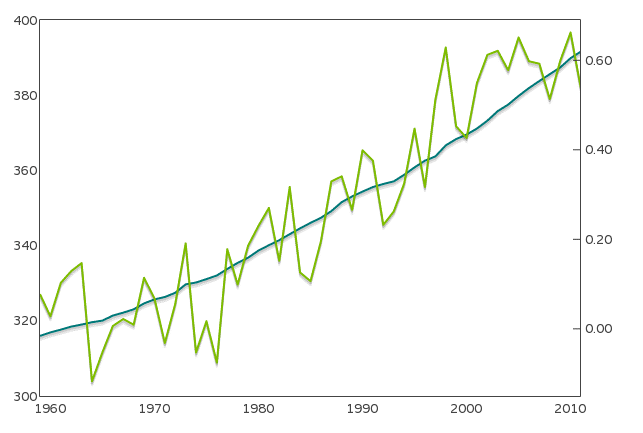
图2 折线图 [注释1]
Pie Chart饼图是一种应该避免使用的图表,因为肉眼对面积大小不敏感。一般情况下,总是应该用柱状图替代饼图。左侧饼图的五个色块的面积排序,不容易看出来(图3a)。换成柱状图就容易多了(图3b)。一般情况下,总是应该用柱状图替代饼图。但是有一个例外,就是反映某个部分占整体的比重,比如贫穷人口占总人口的百分比(图3c)。
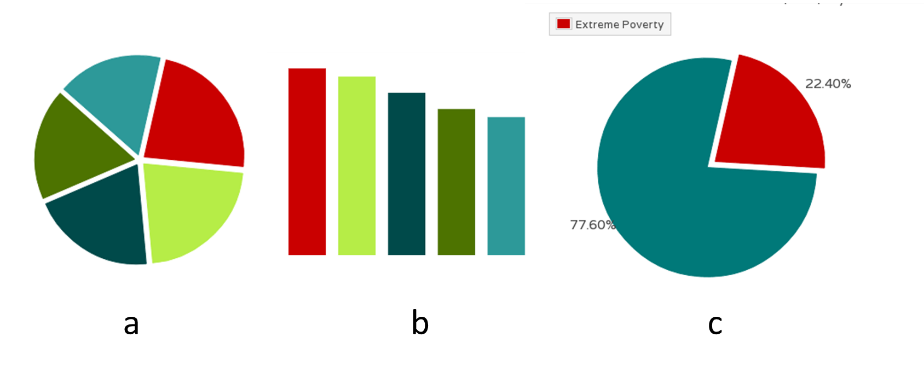
图3 饼图 [注释1]
Scatter Chart散点图适用于三维数据集,但其中只有两维需要比较。图4a是各国的医疗支出与预期寿命,三个维度分别为国家、医疗支出、预期寿命,只有后两个维度需要比较。为了识别第三维,可以为每个点加上文字标示,或者不同颜色(图4b)。
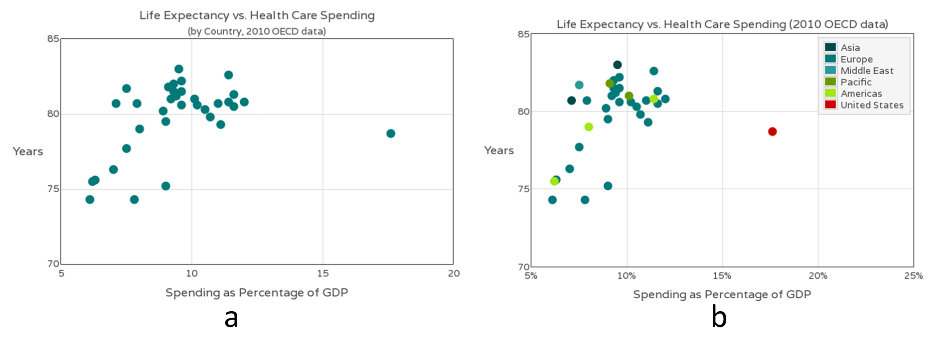
图4 散点图 [注释1]
Bubble Chart气泡图是散点图的一种变体,通过每个点的面积大小,反映第三维。因为肉眼对面积大小不敏感。气泡图只适用不要求精确辨识第三维的场合。图5a是卡特里娜飓风的路径,三个维度分别为经度、纬度、强度。点的面积越大,就代表强度越大。如果为气泡加上不同颜色(或文字卷标),气泡图就可用来表达四维数据。比如图5b就是通过颜色,表示每个点的风力等级。
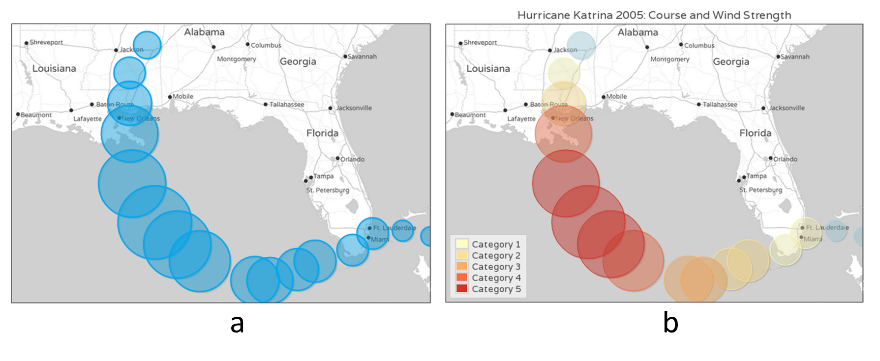
图5 气泡图 [注释1]
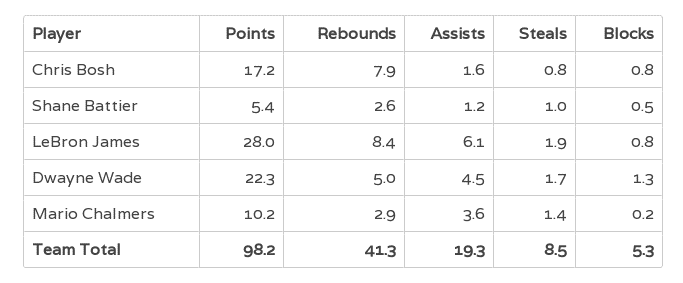
我们前面讲了二维、三维、四维,那么如果更高维度呢?下面是迈阿密热火队首发的五名篮球选手的数据。除了姓名,每个数据点有五个维度,分别是得分、篮板、助攻、抢断、封盖。 如何可视化成图?
Radar Chart雷达图适用于多维数据(四维以上),且每个维度必须可以排序(国籍就不可以排序)。面积越大的数据点,就表示越重要(图6)。但是,它有一个局限,就是数据点不宜过多,否则无法辨别,因此适用场合有限。
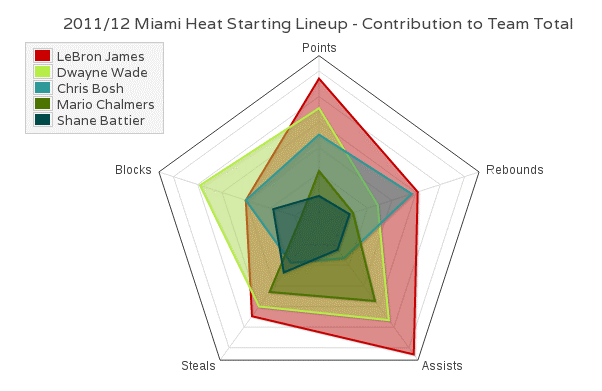
图6 雷达图 [注释1]
下表是对基本图表的一个总结。接下来介绍高级图表。
表1 基本图表小结 [注释2]
| 图表类型 | 数据维度 | 注意事项 |
| 柱状图 | 二维 | 只需比较其中一维 |
| 折线图 | 二维 | 适用于较大的数据集 |
| 饼图 | 二维 | 只适用反映部分与整体的关系 |
| 散点图 | 二维或三维 | 有两个维度需要比较 |
| 气泡图 | 三维或四维 | 其中只有两维能精确辨识,或者说气泡面积不能精确辨识 |
| 雷达图 | 四维以上 | 数据点建议不超过6个 |
高级图表 [注释3]
Tree map树图使用方块的大小和颜色表达每一个entity的至少两个属性的数据。比如图7中就显示了美国各个州的人口数量和人口增长率。可以发现加州、德州都是人口大州。
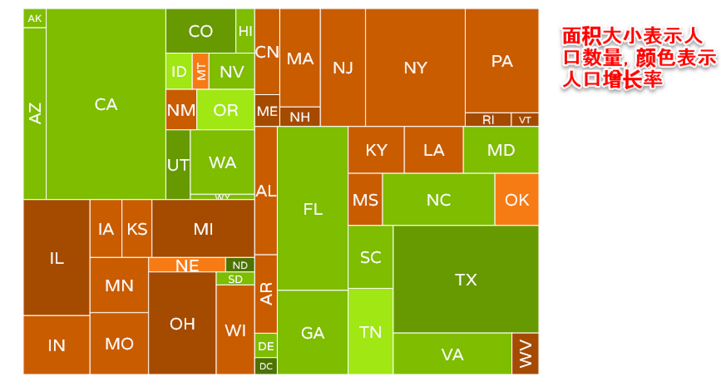
图7 Tree map [注释4]
Scatterplot Matrix散点阵列图可以表达多个变量之间的关系。这里展出的图8可以表达4个变量两两之间的关系。
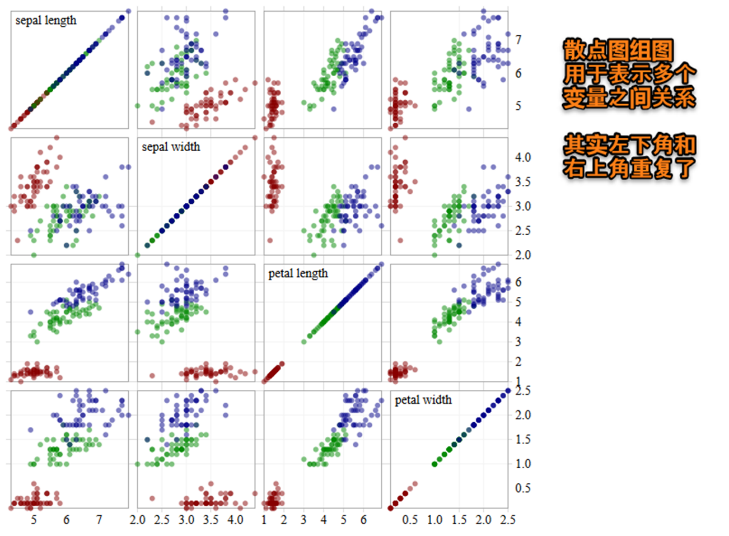
图8 Scatterplot Matrix [注释4]
Parallel Coordinates。与Scatterplot Matrix的功能类似,Parallel Coordinates可以用来可视化多变量之间的关系。图9则表示了7个变量之间的关系,图中的每一条线代表了数据表中的一行数据(a single observation)。显然,如果在两个变量之间的连线相互交叉的情况很多,则表明这两个变量是负相关的关系。
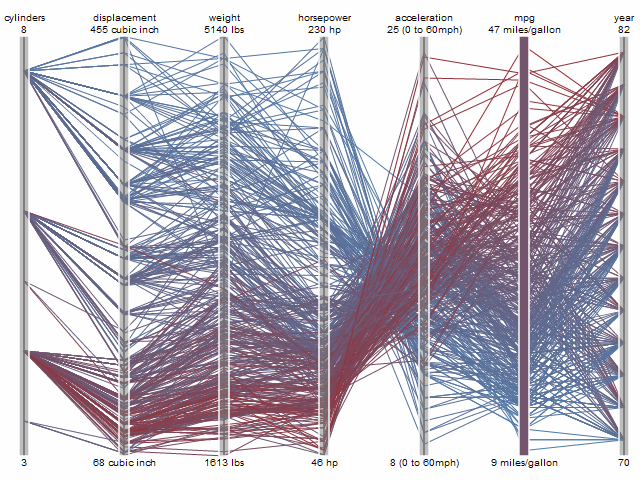
图9 Parallel Coordinates [注释5]
Sankey diagrams桑基图可以可视化网络中节点之间的各种“流”。图10就表达了2050年英国能量生产和能力消耗的模拟结果。图左边是能量供给,右边是能量需求,中间的节点则表达了能量在最终消耗之前是如何被转化和传输的。每个条带的厚度表示了能量“流”的大小。
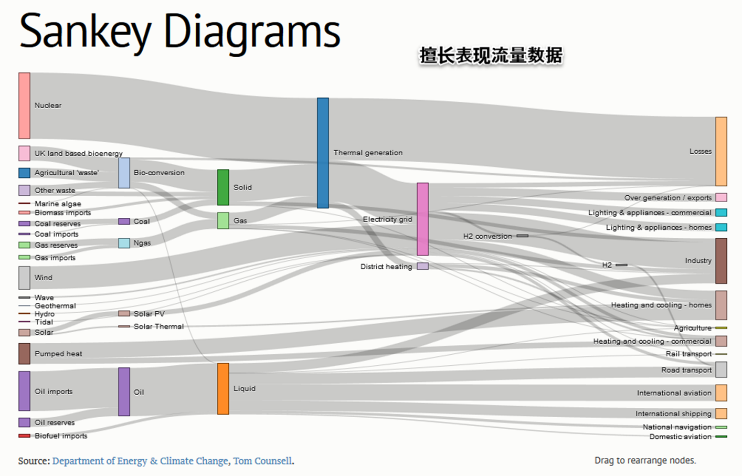
图10 Sankey diagrams [注释4]
Circos Chart圆圈上各个文字指的是美国的各种political action committee,为所支持的国会公职候选人筹集资金的政治行动委员会(图11)。圆圈内的各个圆圈则是国会的议员,面积大小表现所募集资金的多少,颜色表示党派。外围圆圈以及圈外的文字则表示募集资金的来源。
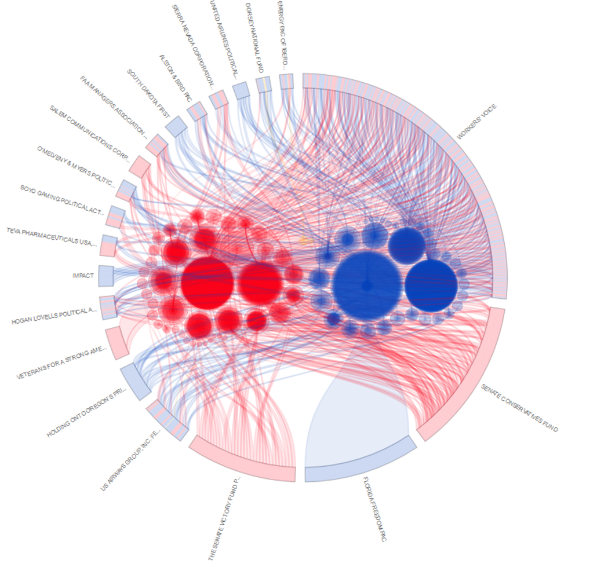
图11 Calendar chart [注释4]
Arc Diagrams。Arc Diagram使用弧线连接一维直线上不同节点来表达信息。比如图12就表达了美国因为枪杀而造成的损失。图中每一条线代表一个人,橙色部分表示这个人活着的时间,灰色部分表示这个人因为被枪杀而失去的“岁月”。换句话说,如果没有被枪杀,这个人可以继续活灰色部分所表示的时间。
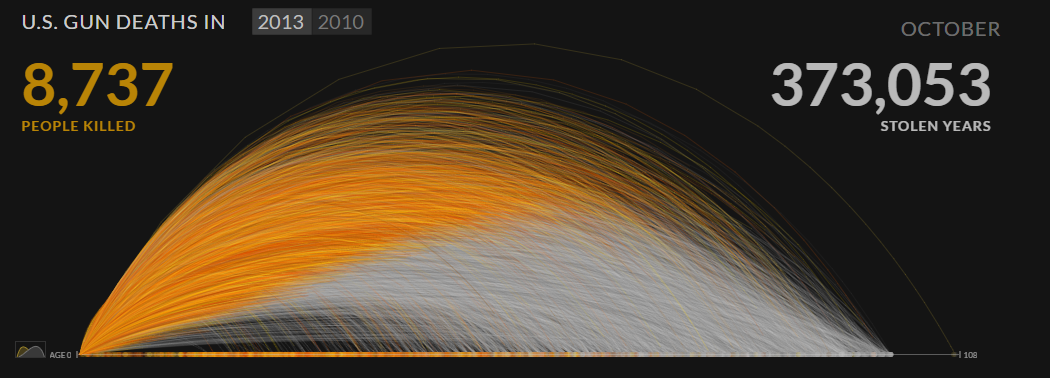
图12 Calendar chart [注释6]
Force-directed graph。图13表达了悲惨世界中各个角色共同出现的次数,这样可以立即定位主角或者核心人物。
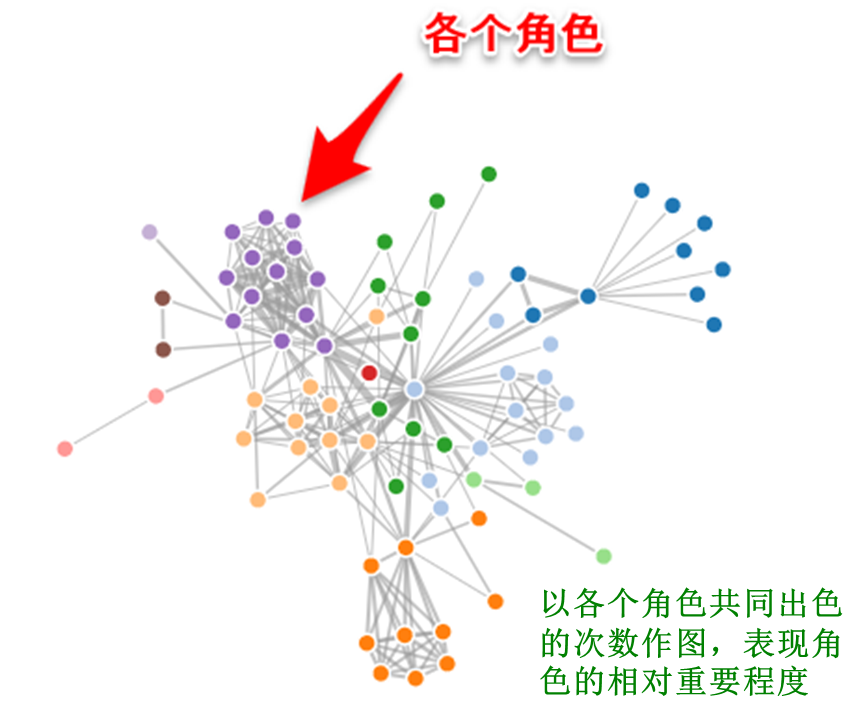
图13 Force-directed graph [注释4]
Calendar chart日历图。图14表示的道琼斯指数的日际、月际、年际变化。一般的折线图只能表示单一时间尺度的数据,比如日际、月际、或者年际变化。但这个日历图则把不同时间尺度的变化放到一起,并且以一种我们日常所常见的日历的格式表现出来。
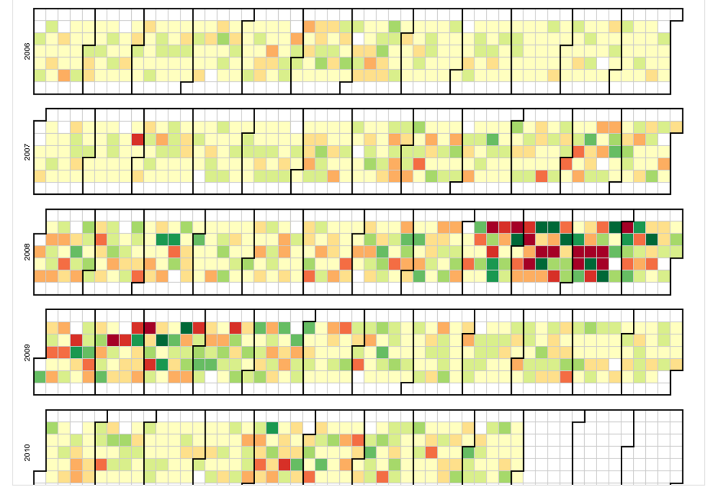
图14 Calendar chart [注释4]
这一期对数据可视化类型的介绍到这里就基本讲完了。数据可视化在城市科学中还有很多其他有趣的话题,有机会将在以后的文章中与大家分享。
来源注释:
1. Thomas, S. A. (2015). Data Visualization with JavaScript. No Starch press.
2. 此部分内容原始来源为注释1, 后经阮一峰博客文章“数据可视化:基本图表” (url: http://www.ruanyifeng.com/blog/2014/11/basic-charts.html)翻译。
3. 编者曾经在香港大学建筑学院城市规划与设计系的“Peer Talk @ New Urban Researcher Seminar Series”2015年系列讲座中讲过本期文摘的内容。
4. Bostock, M. D3 Gallery. https://bost.ocks.org/mike/sankey/
5. Heer, J., Bostock, M., Ogievetsky, V. A tour through the visualization zoo. http://homes.cs.washington.edu/~jheer/files/zoo/.
6. Periscopic. http://guns.periscopic.com/?year=2013.
此版本为文章的最新版本,其他如微信、微博、Facebook以及其他授权发布的文章如有差异,以此最新版本为准。
刘建政
香港大学城市规划与设计系博士后研究员、剑桥大学土地经济系访问学者。本科毕业于华东师范大学地理信息系统专业;硕士毕业于北京大学城市与区域规划专业;博士毕业于香港大学城市规划与设计系。他的个人网站是http://www.jzliu.net/。





